前回はMove it!を使ってアームを任意座標に持ってくるプログラムを作成したが、
残念ながら応答速度が非常に遅い事 & 移動できない座標位置が非常に多く現状使い物にならなかった。
なので、Move It!を使わずにCRANE+に適した形で逆運動学を解いてサーボモータ角度を直接制御するアプローチをトライしてみた。
CRANE+に対する逆運動学アプローチ
物理系は素人なので、まずは逆運動学(Inverse Kinematics)の算出方法の勉強から。
•順運動学 … 関節サーボの目標角度から指先の座標がどの様になるかを算出する問題
•逆運動学 … 指先の目標座標から間接サーボの角度を算出する問題
という事。解き方としては幾何学的にN個の連立方程式を解く問題が一般的な様ですね。当然ながら、複数解は発生するし、関節の多いアームほど計算が複雑になってくる訳で、なかなか素人では難しい。
しかし、このCRANE+はアーム部は4軸と自由度が少なめなので、これを利用して簡略化して考えてみた。アームの構成をおさらいすると、以下のサイトを参照頂きたい。
まず、水平方向の制御はアーム根本のサーボモータ(Joint1)のみなので、水平方向(xy平面)の座標軸からサーボモータ角度は一意に決まる。一方、垂直方向を決めるサーボモータ数は3軸(つまり3変数)だが、2軸(Joint2/Joint3)をアーム位置制御用、1軸(Joint4)をアーム角度制御用という様に役割分担をすれば、単純化できそう!
という事でトライ!
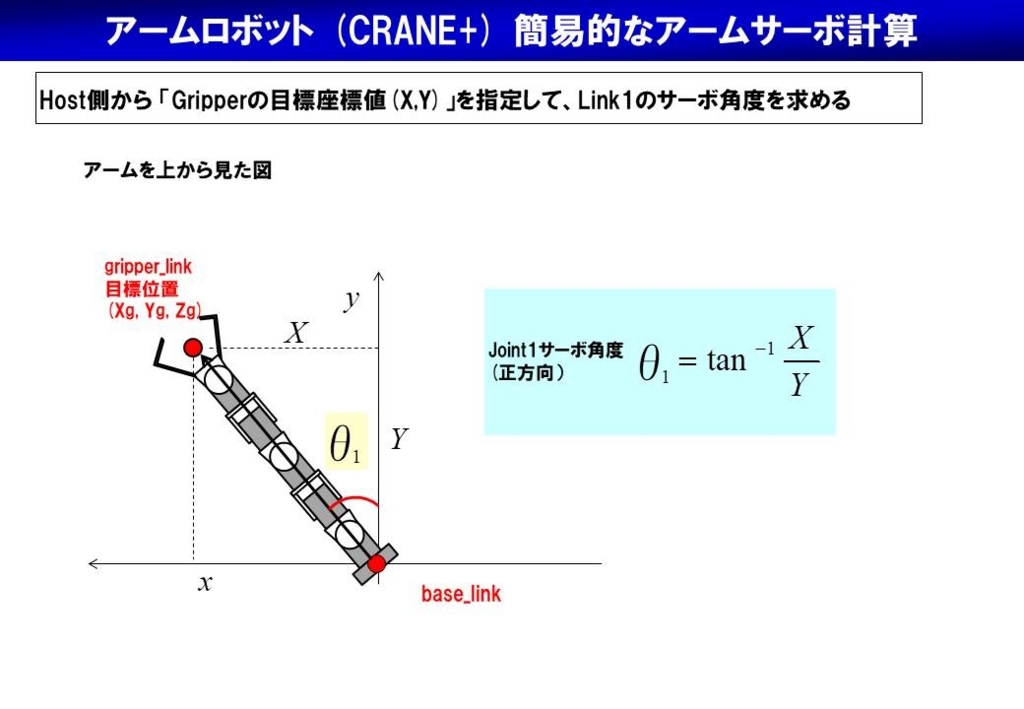


高校数学で勉強した余弦定理を使えば、とりあえず計算出来た!
これをコード実装した。一部抜粋。
#define L_B2 0.076 // base_link〜Shoulder(id2)のLink長さ
#define L_23 0.0825 // Shoulder(id2)~Elbow(id3)のLink長さ
#define L_34 0.094 // Elbow(id3)〜Wrist(id4)のLink長さ
#define L_4G 0.10 // Wrist(id4)〜Gripper_link先のLink長さ
void ArmCtrlTrack::timerCallback(const ros::TimerEvent&){
// JOYCONからの操作情報をアップデート(ARM)
if(pos_delta.x !=0 || pos_delta.y != 0 || pos_delta.z != 0){
arm_pose.pose.position.x += pos_delta.x;
arm_pose.pose.position.y += pos_delta.y;
arm_pose.pose.position.z += pos_delta.z;
ROS_WARN("[Manual]Move Arm_position[%f, %f, %f]", arm_pose.pose.position.x, arm_pose.pose.position.y, arm_pose.pose.position.z);
}
arm_MoveIK(arm_pose.pose.position, wrist_arg, &servo_arg);
}
void ArmCtrlTrack::arm_MoveIK(const geometry_msgs::Point gripper_position, const float wrist_arg, CraneARM_Servo_Arg *servo_arg){
float theta_2d, theta_3d, theta_4d;
float R_24 = sqrt(pow(gripper_position.x,2)+pow(gripper_position.y,2))-L_4G*cos(wrist_arg);
float Z_24 = gripper_position.z + L_4G*sin(wrist_arg)- L_B2;
theta_2d = acos((pow(L_23,2)-pow(L_34,2)+pow(R_24,2)+pow(Z_24,2))/(2*L_23*sqrt(pow(R_24,2)+pow(Z_24,2))));
theta_3d = acos((pow(L_34,2)-pow(L_23,2)+pow(R_24,2)+pow(Z_24,2))/(2*L_34*sqrt(pow(R_24,2)+pow(Z_24,2))));
theta_4d = atan2(Z_24, R_24);
servo_arg->id2.data = theta_2d + atan2(Z_24, R_24)-M_PI/2;
servo_arg->id3.data = theta_2d + theta_3d;
servo_arg->id4.data = theta_4d-theta_3d+wrist_arg;
servo_arg->id1.data = atan2(gripper_position.y, gripper_position.x);
//ROS_WARN("[calc] id2:%f, id3:%f, id4:%f", servo_arg->id2.data, servo_arg->id3.data, servo_arg->id4.data);
//ROS_WARN("[calc] id1:%f", servo_arg->id1.data);
// サーボ角度Publish
if(servo_arg->id4.data >= -M_PI/2 ||servo_arg->id4.data <= M_PI/2) joint4_pub.publish(servo_arg->id4);
if(servo_arg->id3.data >= -M_PI ||servo_arg->id3.data <= M_PI) joint3_pub.publish(servo_arg->id3);
if(servo_arg->id2.data >= -M_PI/2 ||servo_arg->id2.data <= M_PI/2) joint2_pub.publish(servo_arg->id2);
joint1_pub.publish(servo_arg->id1);
return;
}解けない場合は servo_arg->idx.data = nan になるので、その場合はPublishさせない様にしないといけない点に注意。